3267. D-query

Given a sequence of n numbers a₁, a₂, ..., a_n and a number of d-queries. A d-query is a pair (i, j) (1 ≤ i ≤ j ≤ n). For each d-query (i, j), you have to return the number of distinct elements in the subsequence a_i, a_i+1, ..., a_j.

Input.

Line 1: n (1 ≤ n ≤ 30000).

Line 2: n numbers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁶).

Line 3: q (1 ≤ q ≤ 200000), the number of d-queries.

In the next q lines, each line contains 2 numbers i, j representing a d-query (1 ≤ i ≤ j ≤ n).

Output. For each d-query (i, j), print the number of distinct elements in the subsequence a_i, a_i+1, ..., a_j in a single line.

Sample Input

5

1 1 2 1 3

3

1 5

2 4

3 5

Sample Output

3

2

3

РЕШЕНИЕ

структуры данных – дерево отрезков

Анализ алгоритма

Задана статическая (не меняющаяся) последовательность a₁, a₂, ..., a_n. Необходимо выполнить q запросов (i, j): найти количество различных чисел на промежутке a_i, a_i+1, ..., a_j.

Построим массив запросов и отсортируем их по правому концу. К каждому запросу добавим его номер id.

В ячейке posOfLast[i] будем хранить индекс последнего просмотренного элемента i. Проинициализируем их нулями, считая что сначала эти значения не определены.

Построим дерево отрезков b[1..n], изначально занесем в него нули. Последовательно перебираем слева направо числа a₁, a₂, ..., a_n. Пусть текущим является число a_i. Если оно уже раньше встречалось (posOfLast[a_i] содержит не 0), то уменьшим b[posOfLast[a_i]] на 1. Далее увеличим на 1 значение b[i] и установим posOfLast[a_i] равным i. Таким образом значения b_i равны 0 или 1. После обработки числа a_i выполняем все такие запросы q[l; r], для которых r = i: ответом за запрос является сумма b_l + b_l+1 + … + b_r.

Фактически входной массив на каждой итерации изменяется следующим образом:

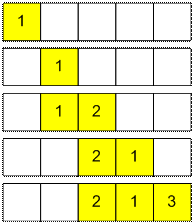
В массиве b, который моделируется деревом отрезков, на каждой непустой позиции стоит единица, а в каждой пустой – нули.

Пример

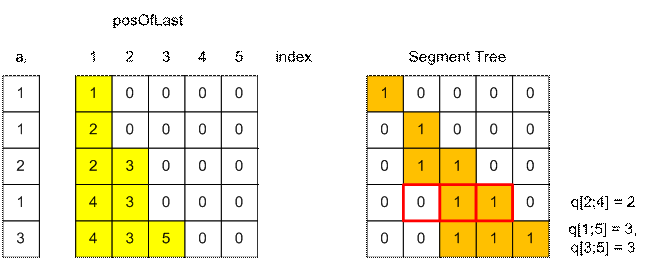
Реализация алгоритма

#include <cstdio>

#include <cstring>

#include <vector>

#include <algorithm>

#define MAX 1000010

using namespace std;

int SegTree[4*MAX];

void SetValue(int Vertex, int LeftPos, int RightPos,

int Position, int NewValue)

{

if (LeftPos == RightPos) SegTree[Vertex] = NewValue;

else

{

int Middle = (LeftPos + RightPos) / 2;

if (Position <= Middle)

SetValue(2*Vertex, LeftPos, Middle, Position, NewValue);

else

SetValue(2*Vertex+1, Middle+1, RightPos, Position, NewValue);

SegTree[Vertex] = SegTree[2*Vertex] + SegTree[2*Vertex+1];

}

}

int Summa(int Vertex, int LeftPos, int RightPos, int Left, int Right)

{

if (Left > Right) return 0;

if ((Left == LeftPos) && (Right == RightPos)) return SegTree[Vertex];

int Middle = (LeftPos + RightPos) / 2;

return Summa(2*Vertex, LeftPos, Middle, Left, min(Right,Middle)) +

Summa(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right);

}

int ans[200010];

int i, n, l, r, q, val;

struct Query

{

int l, r, id;

Query(int l, int r, int id) : l(l), r(r), id(id) {};

int operator <(const Query &a) const

{

return r < a.r;

}

};

vector<Query> qu;

int qPtr, a[MAX], posOfLast[MAX];

int main(void)

{

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d", &a[i]);

memset(SegTree,0,sizeof(SegTree));

scanf("%d",&q);

for(i = 0; i < q; ++i)

{

scanf("%d %d",&l,&r);

qu.push_back(Query(l,r,i));

}

sort(qu.begin(),qu.end());

memset(posOfLast,0,sizeof(posOfLast));

for(i = 1, qPtr = 0; qPtr < q; qPtr++)

{

for(; i <= qu[qPtr].r; i++)

{

val = a[i];

if (posOfLast[val] != 0)

SetValue(1,1,n,posOfLast[val],0);

posOfLast[val] = i;

SetValue(1,1,n,posOfLast[val],1);

}

int Left = qu[qPtr].l;

int Right = qu[qPtr].r;

int Id = qu[qPtr].id;

ans[Id] = Summa(1,1,n,Left,Right);

}

for(i = 0; i < q; ++i)

printf("%d\n",ans[i]);

return 0;

}